Background

On October I have participated in MSHP CTF and one of the challenges intrigued me so much that I promised myself to create a separate article on that.

Challenge

Following screen is my recreation of the challenge. Original application made by Michał Bentkowski.

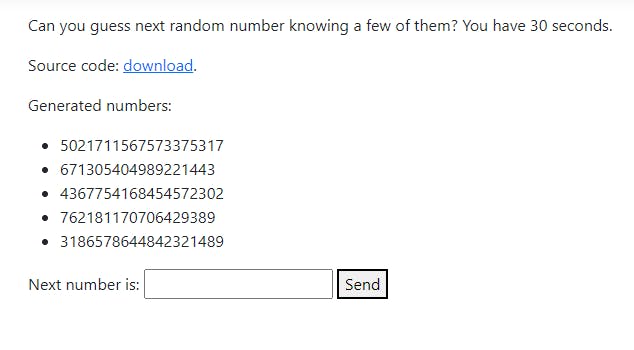
Pasted image 20221108215412.png

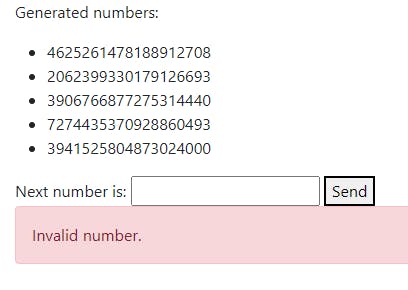
Goal: We are presented with the sequence of 5 random numbers, and we had to guess the sixth one.

Recon

Website

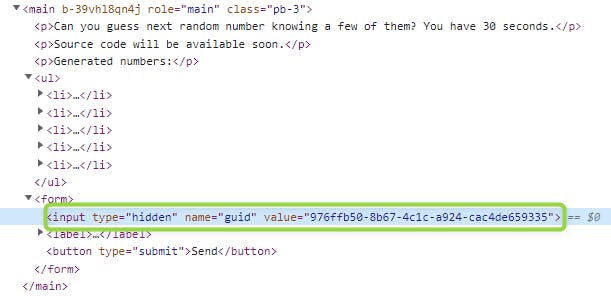
Web source code reveals hidden input containing some kind of validation token. Pasted image 20221108220815.png

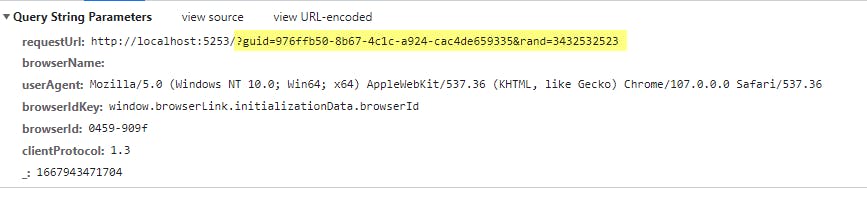
When sending a request, guid is sent together with the guessed number in GET parameters. Pasted image 20221108233442.png

When GUID is invalid or 30 seconds passed: Pasted image 20221108234324.png

When we provide wrong number, but within 30s of generation: Pasted image 20221108234250.png

There is nothing more to see here, so let's switch to the downloadable part.

Source Code

Application appears to be pretty simple .NET Core MVC Application with Razor pages with a lot of default boilercode. Upon closer inspection following key areas have been identified:

Index.cshtml

<p>Generated numbers:</p>
<ul>
    @foreach (var num in Model.Random.RandomNumbers)
    {
        <li>@num</li>
    }
</ul>
<form>
    <input type="hidden" name="guid" value="@Model.Random.Guid">
    <label>
        Next number is:
        <input type="number" name="rand">
    </label>
    <button type="submit">Send</button>
</form>

@if (Model.InvalidGuid)
{
    <div class="alert alert-danger">Invalid GUID.</div>
}
@if (Model.InvalidRandom)
{
    <div class="alert alert-danger">Invalid number.</div>
}
@if (Model.Solved)
{
    <div class="alert alert-success">The flag is @Model.Flag</div>
}

HomeController.cs / Index action

public IActionResult Index(Guid guid, long rand)
{
    var model = new HomeModel
    {
        Random = GenerateRandomModel(),
        Flag = Flag,
        SourceCodeUrl = SourceCodeUrl,
        CacheExpiration = CacheExpiration
    };

    if (guid != default)
    {
        var (invalidGuid, invalidRandom, solved) = CheckSolution(guid, rand);
        model.InvalidGuid = invalidGuid;
        model.InvalidRandom = invalidRandom;
        model.Solved = solved;
    }

    return View(model);
}

HomeController.cs / Validator

private (bool InvalidGuid, bool InvalidRandom, bool Solved) CheckSolution(Guid guid, long rand)
{
    var validGuid = memoryCache.TryGetValue<RandomModel>(guid, out RandomModel randomModel);

    if (!validGuid)
    {
        return (InvalidGuid: true, InvalidRandom: false, Solved: false);
    }
    if (randomModel.ExpectedRandomNumber == rand)
    {
        return (InvalidGuid: false, InvalidRandom: false, Solved: true);
    }
    return (InvalidGuid: false, InvalidRandom: true, Solved: false);
}

HomeController.cs / RNG

private RandomModel GenerateRandomModel()
{
    var guid = Guid.NewGuid();
    // The app runs on .NET Core 6
    var r = new System.Random();
    var randomNumbers = new List<long>();
    for (var i = 0; i < NUM_COUNT; ++i)
    {
        randomNumbers.Add(r.NextInt64());
    }
    var expectedRandom = r.NextInt64();
    var randomModel = new RandomModel
    {
        ExpectedRandomNumber = expectedRandom,
        Guid = guid,
        RandomNumbers = randomNumbers,
    };
    memoryCache.Set(guid, randomModel, TimeSpan.FromSeconds(CacheExpiration));
    return randomModel;
}

Here we can see how guid is used to validate answer, timescoping the solution by purging values from cache after 30 seconds.

The most important seems to be comment content in random number generator - which says that the application is running on .NET Core 6. When you search what's so special about randoms in .NET Core 6, you could find that it has more secure and reliable implementation than .NET Framework, in which Random instance is seeded with current clock ticks - and that clock has finite resolution. Which means in .NET Framework, random instances generated within the same clock "cycle" would return the same "random" values.

Upon reading that, I considered this comment is to indicate that we should not bother cracking random by predicting .NET Framework Random.

I started digging up some .NET MVC vulnerabilities. I've discovered a technique called ASP.NET Overposting and tried naively to manipulate HomeModel by forcing it to assume Solved = true. Of course, that was not meant to work because it is a GET request and no one is updating anything.

The trick is, that The app runs on .NET Core 6 comment was actually a nudge, not discouragement.

.NET Core Sources

The first step to solving the challenge was to find how randoms are generated in .NET Core 6. Because source code is open source for couple years now we can easily find that definition on the GitHub or on .NET Source Browser. I strongly recommend second one.

Navigating to the Random class, we can see that they are using an implementation of xoshiro256** algorithm.

//System.Random.Xoshiro256StarStarImpl
internal sealed class XoshiroImpl : ImplBase
{
    private ulong _s0, _s1, _s2, _s3;

    public unsafe XoshiroImpl()
    {
        ulong* ptr = stackalloc ulong[4];
        do
        {
            // Sys.GetNonCryptographicallySecureRandomBytes(..)
            Interop.GetRandomBytes((byte*)ptr, 4 * sizeof(ulong));
            _s0 = ptr[0];
            _s1 = ptr[1];
            _s2 = ptr[2];
            _s3 = ptr[3];
        }
        while ((_s0 | _s1 | _s2 | _s3) == 0); // at least one value must be non-zero
    }

    //...

    public override long NextInt64()
    {
        while (true)
        {
            ulong result = NextUInt64() >> 1;
            if (result != long.MaxValue)
            {
                return (long)result;
            }
        }
    }

    internal ulong NextUInt64()
    {
        ulong s0 = _s0, s1 = _s1, s2 = _s2, s3 = _s3;

        ulong result = BitOperations.RotateLeft(s1 * 5, 7) * 9;
        ulong t = s1 << 17;

        s2 ^= s0;
        s3 ^= s1;
        s1 ^= s2;
        s0 ^= s3;

        s2 ^= t;
        s3 = BitOperations.RotateLeft(s3, 45);

        _s0 = s0;
        _s1 = s1;
        _s2 = s2;
        _s3 = s3;

        return result;
    }
    //...
}

After clearing the class from comments, attributes and members not related to our case (Random.NextInt64()) implementation looks bearable easy.

Initialize 4 seeds (64 bits) with random bytes.
For each generated random - perform couple bit operations.
Shift right result one bit right.

Now, because we know the four consecutive results of that algorithm, we could traceback the operations and that way get the initial 4 values that that instance of the Random class in the challenge got seeded with.

But how to do it?

Z3 Prover

After the competition ended, I've read the following message:

with z3 everything is easy

What is that z3? Quick research and I found that Z3 is a theorem prover from Microsoft Research.

And it is freaking awesome. With it, you can solve simple equations, or more complicated with multiple unknowns (and multiple solutions). You can solve sudoku or nonograms. Einstein quiz. You name it.

It has libraries (bindings, as they are called on GitHub) for

.NET
C / C++
Java
OCaml
Python
Julia
Web Assembly / TypeScript / JavaScript
Smalltalk (Pharo / Smalltalk/X)

As far as I know, it has one weakness.

Pasted image 20221115220906.png Image source

It is power/logarithm operations.

I have created a little demo when learning how to use Z3 in .NET and it is available here. Official examples are also very comprehensive.

Solution

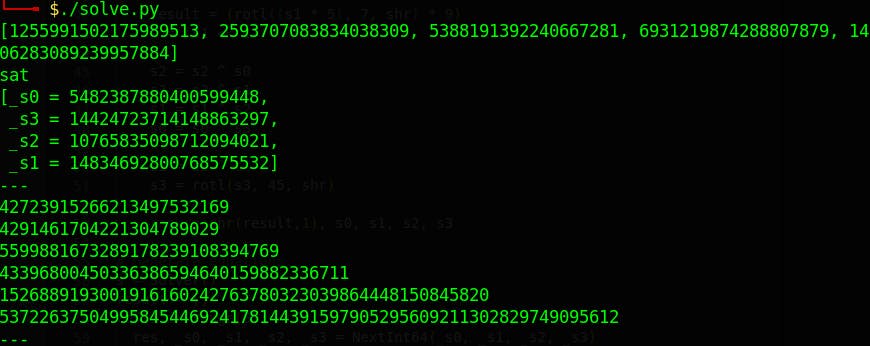
#!/usr/bin/python
# Original solution by Gynvael (https://gynvael.coldwind.pl/?id=756)
import sys
from z3 import *

# Known, consecutive randoms
values_str = """
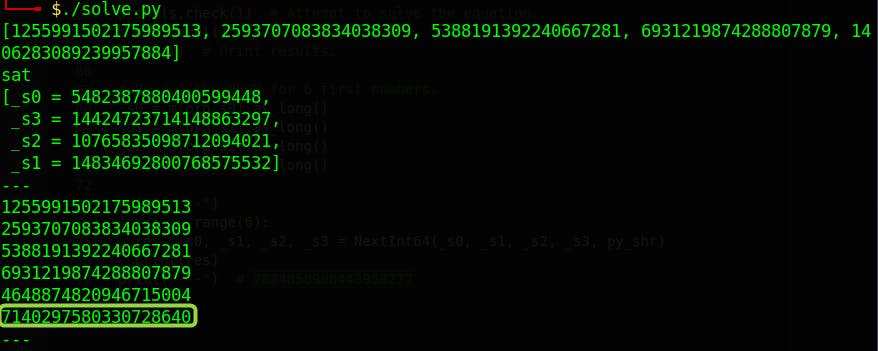
1255991502175989513
2593707083834038309
5388191392240667281
6931219874288807879
1406283089239957884
"""

values = [int(x) for x in values_str.split()]
print(values)

# Interop.GetRandomBytes(..)
org_s0 = BitVec("_s0", 64)
org_s1 = BitVec("_s1", 64)
org_s2 = BitVec("_s2", 64)
org_s3 = BitVec("_s3", 64)

# _sN = ptr[N]; N=0..3
_s0 = org_s0
_s1 = org_s1
_s2 = org_s2
_s3 = org_s3

def py_shr(x, k):
  return x >> k

# https://www.geeksforgeeks.org/python3-program-to-rotate-bits-of-a-number/
def rotl(x, n, shr):
    return (x << n) | shr(x, 64 - n) & 0xffffffffffffffff

def NextInt64(_s0, _s1, _s2, _s3, shr = LShR):
    s0 = _s0
    s1 = _s1
    s2 = _s2
    s3 = _s3

    result = (rotl((s1 * 5 & 0xffffffffffffffff), 7, shr) * 9) & 0xffffffffffffffff
    t = (s1 << 17) & 0xffffffffffffffff

    s2 = s2 ^ s0
    s3 = s3 ^ s1
    s1 = s1 ^ s2
    s0 = s0 ^ s3

    s2 = s2 ^ t
    s3 = rotl(s3, 45, shr)

    return shr(result,1), s0, s1, s2, s3

# Create solver and feed it with known values
s = Solver()
result = []
for i in range(5):
  res, _s0, _s1, _s2, _s3 = NextInt64(_s0, _s1, _s2, _s3)
  result.append(res)
  s.add(res == values[i])

# Attempt to solve the equation.
print(s.check())
m = s.model()
print(m)

# Re-run the PRGN for 6 first numbers.
_s0 = m[org_s0].as_long()
_s1 = m[org_s1].as_long()
_s2 = m[org_s2].as_long()
_s3 = m[org_s3].as_long()

print("---")
for i in range(6):
  res, _s0, _s1, _s2, _s3 = NextInt64(_s0, _s1, _s2, _s3, py_shr)
  print(res)
print("---")  # 7824850908443950277

This requires at least some explaination.

`0xffffffffffffffff`

In Python3 integers are limited by the available memory. This is also a reason why Python is so awesome on working with cryptography challenges that revolves around very large powers. By applying bitwise AND (&) to some big number, we can practically limit the size of it. Think of it as a type casting. Here I'm using 64 ones, limiting the length of the result to 64 bits. Without it, predicting randoms would look like this: Pasted image 20221116020010.png

`LShR` and `>>`

For that one, I've decided to ask Gynvael why one time he is using LShR and another time >>. Apparently

>> is an arythmetic shift
LShR is a logical shift Difference between them
>> preserves sign (fills with 1 for negative, fills with 0 for positive number)
LShR does not preserve sign (fills with 0) For example:

Value	Operator	count	result
`10101010`	LShR (logical)	2	`00101010`
`10101010`	>> (arythmetic)	2	`11101010`
`01101010`	LShR	2	`00011010`
`01101010`	>>	2	`00011010`

But why this is required to shuffle these two operators - I still don't know. Maybe he will explain once again 🥲 (sorry!), this time in the comments.

`res,_s0,_s1,_s2,_s3 = NextInt64(_s0,_s1,_s2,_s3)`

It's not intuitive to use global variables in Python. For that reason, we can use functional approach with passing arguments through the function.

Finally, we can get answer Pasted image 20221116020806.png

Solving Equations Like A Pro

Comments

More from this blog

Driver's Shadow: Unmasking the Kernel Intruder

HTB Sherlock: Noted

HTB Sherlock: MisCloud

HTB Sherlock: Litter

Forensics: Tales for the Brave

👆 Access Patron Benefits 👆

Background

Challenge

Recon

Website

Source Code

.NET Core Sources

Z3 Prover

Solution

`0xffffffffffffffff`

`LShR` and `>>`

`res,_s0,_s1,_s2,_s3 = NextInt64(_s0,_s1,_s2,_s3)`

Additional Reading

Command Palette

Comments

More from this blog

👆 Access Patron Benefits 👆

Background

Challenge

Recon

Website

Source Code

.NET Core Sources

Z3 Prover

Solution

0xffffffffffffffff

LShR and >>

res,_s0,_s1,_s2,_s3 = NextInt64(_s0,_s1,_s2,_s3)

Additional Reading

`0xffffffffffffffff`

`LShR` and `>>`

`res,_s0,_s1,_s2,_s3 = NextInt64(_s0,_s1,_s2,_s3)`